Functions - Mathematical View
A function is a mapping that assigns to each element from a given domain some value from another or the same domain.
For example, your final grade for this course will be a function of your performance in homeworks, labs and exams. The scores you get on assignments and exams will be mapped to a value - A, B, C, etc. - that represents your final grade.
Functions can often be described by arrow diagrams.
Mathematical Functions
Mathematical functions defined on infinite domains are
usually drawn as graphs,
e.g., the function that maps each real number x to 
,
or the function that maps x to 
, etc.
The values along the y-coordinate are
defined by an expression in terms of x,
e.g., 
or 
.
Note that not all identities in variables x and y
define a function.
For instance, the formula for a circle,
, describes no function.
Functions - Computational View
We can also think of a function as a (computational) machine that accepts (one or more) arguments as inputs and produces some value as output.
For instance, I use a program that takes a list of exam and assignment scores as input and combines them in a certain way to produce a list of numbers (between 0 and 100) that can then be translated into letter grades. The computation reflects the guidelines announced at the beginning of the semester, e.g., that the exams contribute a fixed percentage to the total score.
Definition of Functions
We use the notation 
to indicate that f is a function from A to B
and denote by f(a) the value that is assigned
to an argument a by f.
For example,
the squaring function is a function 
such that 
, for all real numbers x.
A constant function (on the integers) is a function 
such that f(n) = k, for all integers n,
where k is a fixed value, e.g., k=2.
We call A the domain of the function f, and B, the codomain. We also speak of ``a function from A to B'' or, especially if A=B, ``a function on A.''
Note that a function must assign a value to each domain element, but not all elements of the codomain need be used.
The range of a function f is defined as the collection of all values y in B, such that y=f(x), for some x in A.
In the examples above range and codomain of the function are different.
Sets
Sets are the basic data structures of mathematics.
Intuitively, any ``well-defined'' collection of mathematical objects can be grouped together to form a single object - a set.
Well-known examples of sets from mathematics are the set of integers, the set of rational numbers, and the set of real numbers. In computer science one often deals with sets of strings (also called ``formal languages'') or trees.
All mathematical objects can in principle be described or defined in terms of sets. In that sense sets are the basic building blocks for constructing mathematical (i.e., formal, abstract) objects.
Functions are mathematical objects and can also be described in terms of sets, as we will show below.
Set Theory
The basic (i.e., undefined) concepts of sets theory are sets and the element-relationship.
The symbol 
is commonly used to denote the element-relationship,
and one writes 
to denote the proposition
x is an element of A
(which may be true or false).
A formal exposition of set theory requires one to specify the main properties of sets, and how new sets can be constructed from given ones, by suitable axioms, or postulates.
For example, one fundamental assumption about sets is the following principle of extension:
Two sets A and B are equal, written A=B, if, and only if, they have the same elements.
Examples.
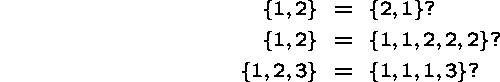
Intuitively, sets are thus unordered collections of objects, where the multiplicities of elements don't matter.
Subsets
Definition.
A set A is a subset of another set B, written, if, and only if, every element of A is also an element of B.
Examples.
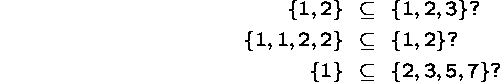
The subset relation is often used to establish equality of sets, based on the following lemma.
Lemma. If and 
,
then A=B.
Proof.
If and ,
then by the definition of the subset relation,
every element of A is an element of B
and
every element of B is an element of A.
This means that A and B have the same elements,
hence are equal.
height6pt width4pt
Proper subsets
We say that A is a proper subset of B,
written 
,
if A is a subset of B,
but not equal to A.
Example.
Be careful about the distinction between the element relation and the subset relation.
Examples.
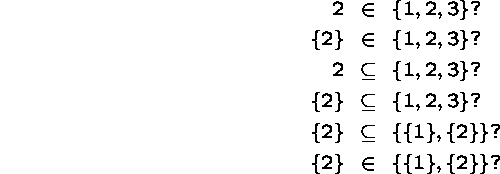
Description of Sets
Finite sets can in principle be described by listing their elements, as we have done in the examples above.
That is, we write
to denote the set consisting of elements 
.
A more general mechanism for describing a set is to characterize via a logical formula a condition its elements have to satisfy:
For every set S and formula P(x) there exists a set, denoted by
that consists of all elements of S for which P is true.
This assumption (about the existence of such sets) is know as the Principle of Comprehension.
Examples of Sets
The (finite) set of integers between -2 and 5:
The (open) interval of real numbers between -2 and 5:
The (infinite) set of even integers:
From a general description it may not always be obvious what the elements of the set are:
Ordered Pairs and Tuples
Sets are unordered collections of elements.
Pairs, or more generally tuples, are ordered collections of elements.
Examples.
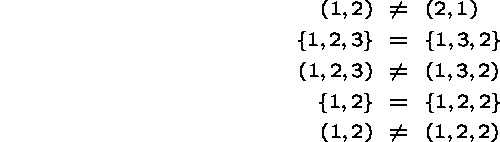
Surprisingly, (ordered) pairs can be defined in terms of (unordered) sets.
In set theory,
an ordered pair (x,y) is taken as an abbreviation
for the set
.
With this definition, do we indeed have
What if x=y?
Tuples can be thought of as ``nested'' pairs. For example, we may regard (1,2,3,4,5) as an abbreviation for (1,(2,(3,(4,5)))) or ((((1,2),3),4),5).
Tuples of different length are never the same.
Cartesian Products
Pairs and tuples provide us with a way of constructing new sets from given ones.
Definition.
If A and B are sets, then there exists a setSymbolically,(read ``A cross B''), called the Cartesian product of A and B, that consists of all ordered pairs (a,b), where
and
.
For example,
if 
and 
,
then
More Set Operations
Other operations for constructing sets include
Let A and B be subsets of some set S. We define:
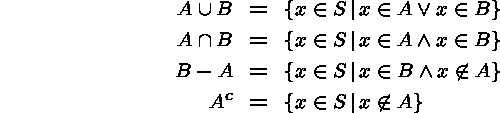
For example, let
S be the set of real numbers,What are
A the set,
B the set.
, 
, B - A, and 
?
Note that set difference can be defined as follows:
Properties of Set Operations
Theorem (properties of the subset relation).
and 
and 
and 
,
then 
.
Proof (of first property).
Let A and B be arbitrary sets. We prove that. Thus x is an element of A. height6pt width4pt
Set Identities
Review the following identities between sets for the next lecture (and observe the similarities to equivalences in propositional logic).
.
.
and 
.
and 
.