Distributivity

Theorem. For all sets A, B, and C,

Proof. Let A, B, and C be arbitrary sets. We show that the two sets and have the same elements:

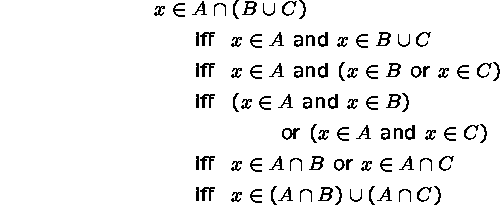
height6pt width4pt

Note the close connection between the ``algebra of sets'' and the ``algebra of propositions'' (Boolean algebra).

Venn Diagrams

Sets can often be conveniently represented by Venn diagrams.

The union of A and B is represented by:

The intersection is represented by:

The set difference B - A is represented by:

Counterexamples for Set Identities

Claim. For all sets A, B, and C,

Is this claim true?

Consider the two Venn Diagrams:

The diagram on the left represents , the one on the right, A - C.

The difference in the diagrams suggests a counterexample to the claim.

Take , , and . Then , whereas .

The Empty Set

A set with no elements is called an empty set.

Theorem. If is an empty set, then , for all sets A.

Proof. It is vacuously true that every element of an empty set is an element of every other set A. height6pt width4pt

Corollary. There is only one empty set.

Proof. Suppose A and B are both empty sets. By the theorem above we have and , and hence A=B. height6pt width4pt

We use the symbol , or sometimes , to denote the (unique) empty set.

Theorem.

Disjoint Sets

Two sets A and B are said to be disjoint if they have no elements in common, i.e., .

Examples.

Is ?
No, .

Is ?
Yes, by previous theorem.

A partition of a set A is a collection of pairwise disjoint sets , such that

For example, at the end of the semester I will partition the class into subsets with grades of A, A-, etc. It will be a partition, since each student gets one, and only one, grade.

Partitions are closely related to equivalence relations, which we will discuss later in the semester.

Powersets

Powerset Axiom.

If A is a set, then there exists a set, called the powerset of A and denoted by the symbol , whose elements are exactly all the subsets of A.

Example. If A is the set , then

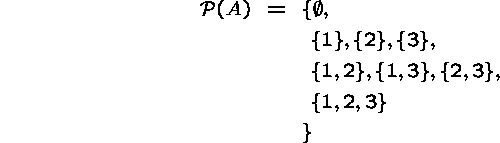
Do we have , or , or ?

No, because , etc.

If A has n elements, how many elements are there in its powerset?

Answer: . Why?

Set-Theoretic Definition of Functions

In mathematics a function is usually thought of as a subset of the cartesian product that satisfies certain properties.

For example, the set

describes a function from to , that maps a to 1, b to 2, and c to 1.

In general, a set of pairs must satisfy two conditions to specify a (total) function:

• Completeness:

  for each element x of the set A, there exists an element y of B, such that the pair (x,y) is in F.

• Uniqueness:

  F does not contain two pairs (x,y) and (x,z), where y and z are different.

Partial Functions

Is the (multiplicative) inverse mapping, which assigns to each rational number m/n the number n/m a function on the rational numbers?

No, because n/m is not defined if m=0.

It is a function on the non-zero rational numbers, though.

When we speak of a function we usually mean a total function, that is, a mapping f that assigns a value from B to each argument from the specified domain A.

In computer science one also often encounters ``partial functions,'' such as division, which may be ``undefined'' for certain arguments.

In set-theoretic terms, a partial function is a subset of that satisfies the uniqueness property, but not the completeness property.

Equality of functions

Two functions f and g from A to B are said to be equal, written f=g, if they agree on all arguments, i.e., f(x)=g(x) for all .

For example, let f and g be functions on the integers such that and g(n) = (n+1)(n-1). Then f=g.

The identity function on a set A is the function such that id(x) = x, for all .

Is the function f on the natural numbers, such that , equal to the identity function on ?

Sequences

A sequence is formally a function on the natural numbers, or some initial segment of the natural numbers.

For example, the infinite sequence

can be thought of as a function f that maps each natural number n to a rational number, .

The finite sequence

can be thought of as a function such that

Arrays are essentially finite sequences, though as a data type they also come with operations for accessing array elements, changing them, etc.

Tuples

We have seen that tuples may be thought of as ``nested pairs.''

Alternatively, a tuple may be defined as a sequence of finite length. More specifically, an n-tuple is a sequence of length n, that is, the domain of the corresponding function has n elements.

The notation is used to denote the set of all n-tuples with the property that the first element is in , the second in , and so on. Sets and may be different, but need not be.

For example, denotes the set of all pairs of integers.

An example of a set of tuples with components of different type is a collection of pairs of names and corresponding ID-numbers.

Multiple-Argument Functions

Functions of two or more arguments may be viewed as standard one-argument functions where the domain is a set of tuples (of fixed length).

For example, a binary function is a function f of type .

Example. The addition function on the integers is a binary function that maps each pair of integers (m,n) to their sum m+n.

In general, by an n-ary function we mean a function of type

the domain of which is a set of n-tuples.

It is of course also possible for the codomain of a function to be a set of pairs or tuples.

For example, we may define a function such that f(m,n) = (q,r), where q and r are the quotient and remainder, respectively, of the integer division of m by n.

Boolean Functions

Truth tables describe functions, called Boolean functions, that map n-tuples of truth values to single truth values.

On the other hand, every propositional formula A defines a truth table, and hence a (unique) Boolean function.

For example, the formula defines the following Boolean function.

One-to-One and Onto Functions

A function is said to be one-to-one (or injective) if, and only if, for all elements x and y in X, we have x=y whenever f(x)=f(y).

Example. Let f and g be functions with domain and co-domain , defined by:

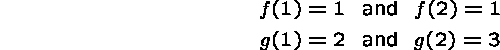
Then g is one-to-one, but f is not.

A function is said to be onto (or surjective) if, and only if, for every element y in Y, there exists an element x in X, such that f(x)=y.

A function is onto iff its range equals its codomain.

For example, the function f from to , defined by:

is surjective, whereas no function from to can possibly be onto.

Permutations

One class of bijective functions are permutations, which rearrange a (finite) sequence of the numbers .

For example, reversing a sequence is a permutation:

or

Another examples is a card shuffle. We can represent the 52 cards in a deck by the numbers . Shuffling corresponds to rearranging a given sequence of these numbers.

This is an example of a perfect shuffle on an eight card deck.

• About this document ...