Defining Functions
Functions with a finite domain can be described by specifying for each element in the domain the associated element in the codomain.
The two basic mechanisms
for defining functions on infinite domains,
such as the natural numbers
![]() ,
are
,
are
An explicit definition of a function f consists of giving an expression that indicates for each domain element x how f(x) is obtained from previously defined functions (including constants) by composition.
Examples.
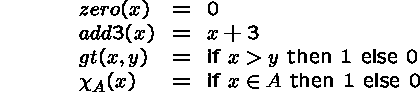
The last function is called the characteristic function of the set A.
If-then-else may be used for case distinctions in function definitions.
Recursive Definitions
A recursive definition of a function consists of giving an expression for every domain element x that indicates how f(x) is obtained from previously defined functions and values of f for ``smaller'' arguments (by composition).
Such definitions are also called recursive. They are based on a recursion principle, which specifies under which conditions such definitions with self-references are well-formed.
For example, the number of permutations of n elements is n! (or fact(n), read n factorial). This function can be defined recursively by:
![]()
The values fact(n), for all n>0, depend on values fact(k), where k is smaller than n.
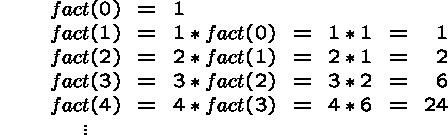
Example: Squares
The same function can usually be defined in different ways.
For instance, the function that squares its argument can be defined explicitly in terms of multiplication,
![]()
or by recursion:
![]()
From the recursive definition we get the following function values:
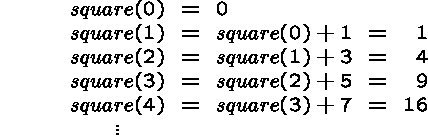
The two definitions above define the same function, as
![]()
or, equivalently,
![]()
Fibonacci Numbers
The recursive definition of the following well-known function employs the function values for several smaller arguments:
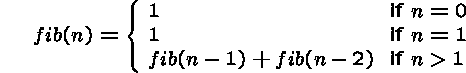
The corresponding function values are called Fibonacci numbers:
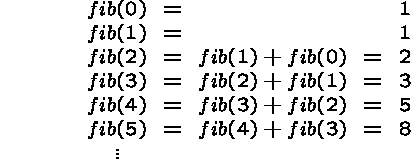
The Fibonacci numbers were originally defined to count the number of rabbits after n generations, but they pop up in an amazing variety of places:
Partially Defined Functions
A key requirement of a recursive definition is that it be formulated in terms of function values for smaller arguments.
Consider this definition,
![]()
and corresponding attempts at computing function values,
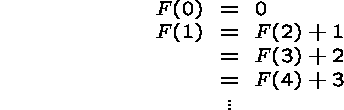
This function is defined for one argument only!
What about the function G, defined for positive integers by
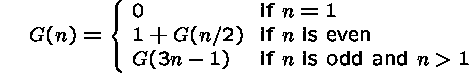
Is it well-defined for all arguments?
We have
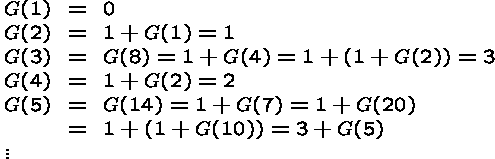
Thus, if G(5) were defined, we could infer the contradictory statement that 0=3! In other words, G(5) must be undefined.
It has been conjectured (and shown up to one trillion) that a slight modification,
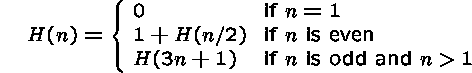
defines a function on all positive integers.
2-1
10-5-16-8-4-2-1
17-52-26-13-40-20-10-5-16-8-4-2-1
21-64-32-16-8-4-2-1
35-106-53-160-80-40-20-10-5-16-8-4-2-1
Note that if this function is well-defined, then the value of H(n) counts the number of downward steps this path takes, i.e H(2) = 1 and H(35) = 10.
Well-Formed Recursive Definitions
A well-formed recursive definition of a function f consists of two parts:
Later on we will see recursive definitions of functions on other domains, such as lists, where ``smaller'' necessarily has to be interpreted differently.
Computing Values of Recursively Defined Functions
The evaluation of a recursively defined function for a specific argument involves two kinds of operations:
Example.
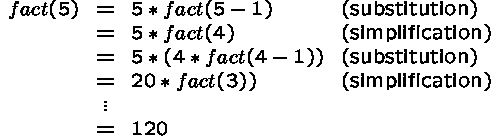
The evaluation process will terminate if the definition is well-formed.
More General Recursive Definitions
Example.
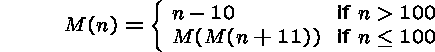
This function is known as ``McCarthy's 91 function.'' Its definition uses nested recursive function applications.
Is this function defined for all arguments ![]() ?
?
Consider one instance,

The function is in fact defined for all positive integers and remarkably takes the value 91 for all arguments less than or equal to 101.
Recursion - Summary
Recursion is a general method for the definition of functions (and also a powerful technique for designing algorithms).
Recursive definitions generally specify only partial functions. (Recall that a partial function satisfies the uniqueness, but not the completeness property required of total functions.)
If a recursive definition employs only values of the defined function for smaller arguments, it defines a total function.
The evaluation of recursively defined function for specific arguments is based on calculation by substitution and simplification.
These two concepts,