The Tower of Hanoi

The tower of Hanoi consists of a fixed number of disks stacked on a pole in decreasing size, that is, with the smallest disk at the top.

There are two other poles and the task is to transfer all disks from the first to the third pole, one at a time without ever placing a larger disk on top of a smaller one.

There is an elegant solution to this problem by recursion.

Tower Moves

First consider how many moves are needed, at the least, to transfer a tower of k disks.

Observe that we need to get to the following intermediate configuration, so as to be able to move the largest disk.

That is, we have to transfer the k-1 smaller disks to the middle pole, can then move the largest disks from the first to the third pole, and finally the k-1 smaller disks from the second pole to the third pole.

Let M(k) be the minimum number of moves required to transfer k disks from one pole to another pole. This function M satisfies the recursive identity,

for all k>0.

In addition, we set M(0) = 0, so that by the above identity M(1)=1, which is correct as one move suffices to transfer a tower containing only a single disk.

Minimum Number of Moves

Let us evaluate the function for some arguments:

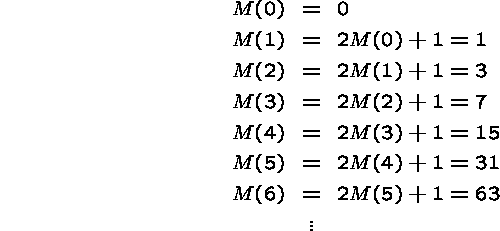
The values grow fairly fast. In fact one can show that the function M can be explicitly defined by

for all . That is, function values grow exponentially with the argument.

This tells us that a lot of moves are needed to transfer a tall tower, though we don't know the actual sequence of moves yet. For that purpose we will write an SML function.

Tuples in ML

ML provides two ways of defining data types that represent sequences.

Lists as we have seen are finite sequences of elements of the same type.

Tuples are finite sequences, where the length is arbitrary but fixed and the different components need not be of the same type.

Some examples of tuples and the corresponding types are:

- val t1 = (1,2,3);
val t1 = (1,2,3) : int * int * int
- val t2 = (4,(5.0,6));
val t2 = (4,(5.0,6)) : int * (real * int)
- val t3 = (7,8.0,"nine");
val t3 = (7,8.0,"nine") : int * real * string

The components of a tuple can be accessed by applying the function #i, where i is a positive number.

- #1(t1);
val it = 1 : int
- #1(t2);
val it = 4 : int
- #2(t2);
val it = (5.0,6) : real * int
- #2(#2(t2));
val it = 6 : int
- #3(t3);
val it = "nine" : string

If a function #i is applied to a tuple with fewer than i components, an error results:

- #4(t3);
... Error: operator and operand don't agree

Tower of Hanoi in ML

We represent a move as a pair of integers (x,y). That is, (x,y) is interpreted as moving a disk from pole x to pole y. Poles are represented by the numbers 1, 2, and 3.

The function ttower takes three integer arguments k, x, and y such that and . It returns a list of moves that transfer a tower of k discs from pole x to pole y.

- fun ttower(k,x,y) =
= if (k=0 orelse x=y) then []
= else if k=1 then [(x,y)]
= else ttower(k-1,x,comp(x,y))
= @ ((x,y)::ttower(k-1,comp(x,y),y));
val ttower = fn : int * int * int
. -> (int * int) list

The second line indicates that no move is needed if k=0 or the tower is to remain at the same pole. The third line provides an explicit solution for moving a tower of one disk. The fourth and fifth line show that in the general case we can (a) move k-1 disks from x to the ``auxiliary'' pole z, (b) move the largest disk from x to y, and (c) move k-1 disks from z to y.

The pair (x,y) is an example of a tuple of length 2 and type int * int.

The function comp, if provided with two of the numbers 1, 2, or 3 as arguments, returns the third.

- fun comp(x,y) = 6-(x+y);
val comp = fn : int * int -> int
- comp(3,1);
val it = 2 : int

Here are some simple sequences of moves,

- ttower(1,1,3);
val it = [(1,3)] : (int * int) list

- ttower(2,2,2);
val it = [] : (int * int) list

and a few longer ones,

- ttower(2,1,3);
val it = [(1,2),(1,3),(2,3)] : (int * int) list

- ttower(3,1,3);
val it = [(1,3),(1,2),(3,2),(1,3),(2,1),(2,3),(1,3)] : (int * int) list

- ttower(4,1,3);
val it = [(1,2),(1,3),(2,3),(1,2),(3,1),
. (3,2),(1,2),(1,3),(2,3),(2,1),
. (3,1),(2,3),(1,2),(1,3),(2,3)]
: (int * int) list

Recursively Defined Sequences

An infinite sequence

is formally a function a defined on the domain of natural numbers (i.e., nonnegative integers) by .

Such sequences are often alternatively specified by recursive identities, or so-called recurrence relations.

In a recurrence relation each term is equated to an expression that may contain (some or all) of the i predecessors , where i is a fixed integer.

The terms , which do not have i predecessors, need to be defined separately by so-called initial conditions.

The recurrence relation for the function M defined above consists of the following identities:

The Fibonacci numbers are characterized by the following recurrence relation:

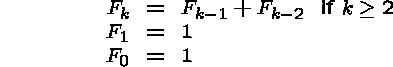
Arithmetic and Geometric Sequences

A sequence is called an arithmetic sequence if there is a constant d such that , for all .

A sequence is called a geometric sequence if there is a constant r such that , for all .

For example, balances in an interest-bearing account in which interest is compounded, will follow a geometric sequence if no deposits or withdrawals are made.

Functions defining arithmetic or geometric sequences can be described explicitly.

We have , for all , for any arithmetic sequence; and , for all , for any geometric sequence.

The latter identities may be viewed as solutions of the respective recurrence relations above.

Methods for solving other kinds of recurrence relations are of relevance to the analysis of algorithms, but will not discussed in this course. Proving that a solution is correct typically requires mathematical induction arguments, a topic we will discuss next.

• About this document ...