The Tower of Hanoi Again

We have seen in the last lecture that the minimum number M(n) of moves required to transfer a tower of n disks satisfies the identity,

for all n>1, with M(1) = 1.

We also claimed, but didn't prove, that

for all .

Let us examine this more closely.

Case n=1. Since

this case is correct.

Assumption. Suppose we already know that , for an arbitrary, but fixed number .

Case n=k+1. We have

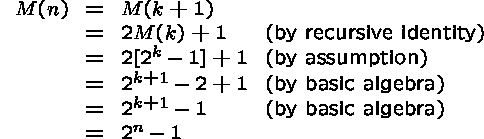
so that this case is also correct, under the above assumption.

Do these arguments amount to a proof?

Mathematical Induction

We did indeed give a correct proof, based on the mathematical induction.

Principle of Mathematical Induction

Let P(n) be a predicate defined on the natural numbers and let a be a fixed natural number. Suppose the following two statements are true:

1. P(a) is true.
2. For all integers , if P(k) true then P(k+1) is true.

Then P(n) is true for all natural numbers n with .

Mathematical induction is a powerful proof technique closely related to recursion.

It is a principle because it can not be derived from other facts, but must be assumed as a basic property of the natural numbers.

Note. The induction principle can be generalized so as to apply to integers, rather than natural numbers.

Induction Proofs

Proofs by mathematical induction consist of two steps:

1. the basis step: proving that P(a) is true; and
2. the inductive step: proving that for an arbitrary, but fixed number , P(n+1) is true whenever P(n) is true.

For example, let P(n) be the property `` '' and let us prove that P(n) is true for all .

Basis step. If n=10, then

Inductive step. Assume P(n) is true for some arbitrary, but fixed integer . We have to show that P(n+1) is true.

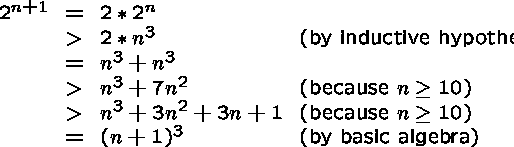
height6pt width4pt

Note that the assumption that P(n) is true is called the inductive hypothesis. It is part of the inductive step.

Induction and Summation

Let P(n) be the property that

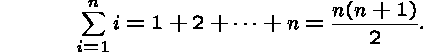
We use induction to prove that P(n) is true for all integers .

Basis step. If n=1, then

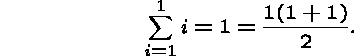
Inductive step. Assume P(n) is true for some arbitrary, but fixed integer . We have to show that P(n+1) is also true under this assumption.

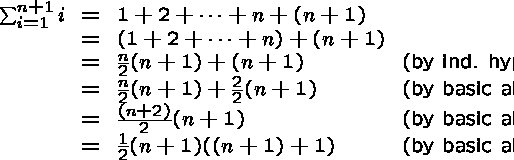
height6pt width4pt

Induction and Divisibility

Let P(n) be the property that `` is divisible by 7.'' We prove that P(n) is true for all nonnegative integers.

Basis step. If n=0, then

which indicates that P(0) is true.

Inductive step. Let n be an arbitrary, but fixed nonnegative integer and suppose is divisible by 7, i.e.,

for some integer k.

We have to show that is divisible by 7.

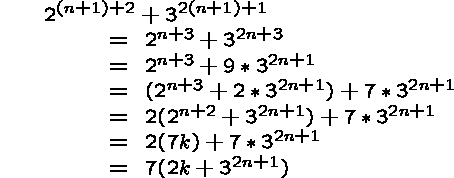
Thus is divisible by 7. height6pt width4pt

The above identities are all based on algebraic manipulations, except one, which uses the induction hypothesis. Which one is it?

Induction and Grading

Students have a habit of complaining about their grades. Such complaints are completely ridiculous for CSE113, for

if one takes any set M of n CSE113 students, all students in the set get the same grade.

This can be proved by induction.

If n=1, then the set M contains only one student, so there is only one grade.

Suppose, as induction hypothesis, that the above assertion is true for any set of n students, where n is a positive integer. We show that the assertion is also true for any set of n+1 students.

Take a set M of n+1 CSE113 students. Since , we have , which means that M contains two members at least. Let a and b be two different students in M.

Both and have n elements, so that we may apply the induction hypothesis to infer that all students in get the same grade, and all students in get the same grade.

Since , it follows that all students in M get the same grade.

In short, in this class everybody gets treated the same way!

The fallacy in the preceding ``proof'' is hidden in the following part:

Since , it follows that all students in M get the same grade.

This argument is only valid if M has at least three elements.

In that case, there is a third student c, who gets the same grade as a and also the same grade as b, from which one can conclude that a and b, and hence all students in M, get the same grade.

There is a gap in the proof for two-element sets M. In that case a and b are the only elements of M, and it is trivially true that all students in , and also all students in , get the same grade. But there is no logical justification for inferring that all students in M (that is, a and b) get the same grade.

Induction and the Fibonacci Numbers

Recall that the Fibonacci numbers are defined recursively:

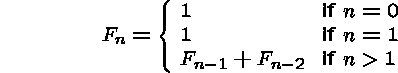
Let be the number .

The size of this number explains why recursive Fibonacci programs run so slowly:

We claim that

for all natural numbers n.

We first prove two basis cases.

If n=0, then

If n=1, then

Next let us assume, for some arbitrary, but fixed positive integer n, that

We show that under these assumptions

More specifically we have

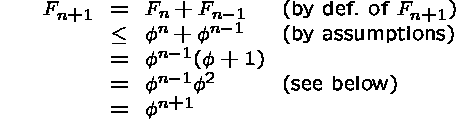
The above proof uses a stronger induction principle that will be discussed in the next lecture.

Note that

• About this document ...