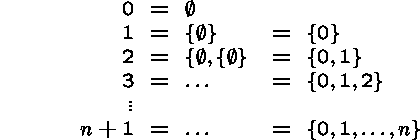
The Natural Numbers in Set Theory
In the last lecture I said that all mathematical objects can in principle be expressed in terms of set theory.
Here is how the natural numbers can be encoded:
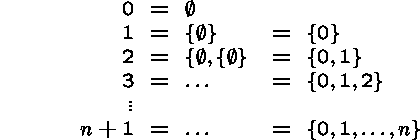
You can see from these definitions why we say ``in principle,'' because the encoding is rather cumbersome.
Russell's Paradox
It is given that the barber of a certain small town shaved all the inhabitants of the town who did not shave themselves, and never shaved any inhabitant who did shave himself.
Does the barber shave himself?
No, because then he is violating the rule of never shaving any inhabitant who did shave himself.
Does he not shave himself?
No, because then he is again violate the rule, because he is failing to shave someone who is not shaving himself.
We have an impossible situation: he neither shaves himself nor does he not shave himself!
What does this have to do with set theory?
Russell's Paradox
The barber of a certain small town got a new contract under which he was to be paid a generous sum at the end of the year provided he shaved all the inhabitants of the town who did not shave themselves, and never shaved any inhabitant who did shave himself.
When trying to collect the money after a year, he was told that nothing was due, because he had shaved himself and therefore had violated the rule of never shaving any inhabitant who did shave himself.
Having learned his lesson, the barber did not shave himself the next year. But at year-end he was turned down again, because this time he had failed to shave someone who did not shave himself.
What should he do?
And what does this have to do with set theory?
Lesson: be careful when signing a contract or you may end up in a difficult situation.
Be also careful when you set up a formal theory, such as set theory, so as to not get into contradictions that cannot be resolved.
Set Theory Paradox
Consider the set of all sets that are not elements of themselves:
Is S an element of itself?
We have
which is a contradiction!
The above definition of S is not covered by the Comprehension Principle. We can only define, for some given set U,
Now,
if 
, then by the (new) definition of S, we get 
,
which is a contradiction.
Thus we must have ,
in which case we may also infer that 
,
for otherwise there is a contradiction.
In short,
we avoid the paradoxical situation
by requiring the additional condition 
.
Do There Exist Any Sets At All?
Set theory is defined by axioms and postulates. From the postulates that we have seen so far one can actually not derive that there exists a set.
Existence Axiom.
There exists a set.
This axiom surprisingly implies that the empty set exists, as the following argument shows.
Suppose there exists a set, say A.
Then by the comprehension principle 
is also a set.
The latter set is the empty set.
Once we know that the empty set exists, we can get the natural numbers and from those practically everything.
More Postulates
When defining the natural numbers by sets, we implicitly used additional postulates.
Pairing Axiom.
If A and B are sets, then there exists a set that contains exactly A and B as elements.
Union Axiom.
If C is any collection of sets, then there exists a set, usually denoted by, that consists of exactly those elements that are elements of at least one set in the collection.
Example. Let C be the collection of three sets,
,
,
and
.
Then
Now we can formally define the natural number n+1 in set theory by:
}