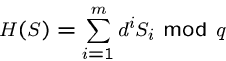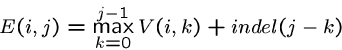

Next: About this document ...
Up: My Home Page
String Comparison
The two ``killer apps'' of modern string processing algorithms have been
computational biology and searching the Internet.
While exact matching algorithms are more important in text processing
than biology, they are important (1) to illustrate
techniques, and (2) as a component of heuristics for approximate matching.
Three primary classes of string matching problems arise, determining
whether preprocessing techniques are appropriate:
- Fixed texts, variable patterns - e.g. search the human genome
or the Bible.
Suffix trees/arrays are data structures to efficiently
support repeated queries on fixed strings.
- Variable texts, fixed patterns - e.g. search a news feed for dirty
words, or the latest Genbank entries for specific motifs.
Such applications justify preprocessing the set of patterns so as
to speed search.
- Variable texts, variable patterns - e.g. the naive
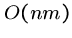 brute force search algorithm.
brute force search algorithm.
Suffix trees solve this problem in linear time, but with excessive complexity
and overhead.
Efficient Exact String Matching
We have seen the naive brute force algorithm searching for pattern  in text
in text  in
in 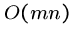 time, where
time, where 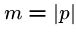 and
and 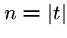 .
.
The brute force algorithm can be viewed as sliding the pattern across
from left to right by one position when we detect a mismatch
between the pattern and the text.
But in certain circumstances we can slide the pattern to the right
by more than one position:
pattern: ABCDABCE
text: ....ABCDABCD....
Since we know the last seven characters of the text must be 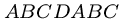 ,
we can shift the pattern four positions without missing any matches.
,
we can shift the pattern four positions without missing any matches.
The Knuth-Morris-Pratt Algorithm
Whenever a character match fails, we can shift the pattern forward
according to the failure function 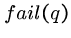 , which is the length
of the longest prefix of
, which is the length
of the longest prefix of 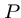 which is a proper suffix of
which is a proper suffix of 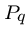
i: 1 2 3 4 5 6 7 8 9 10
P[i]: a b a b a b a b c a
fail[i]: 0 0 1 2 3 4 5 6 0 1
Given this prefix function we can match efficiently - on a character match
we increment the pointers, on a mismatch we slide the pattern one step plus the
failure function.
a b b b a b a b a b a c a b a b a b a b c a
a b *
*
*
a b a b a b a *
*
a b a b a b a b c a
Note that we will not match the pattern from the begining, but according
to where we are in the text - we never look backwards in the text.
Computing the failure function for the pattern can be done in 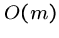 preprocessing, and hence does not change the asymptotic complexity.
preprocessing, and hence does not change the asymptotic complexity.
Time Complexity of KMP
If the pattern rejects near the beginning,
we did not waste much time in the search.
If the pattern rejects near the end (e.g. EEEEEEEH in 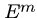 ,
there is an opportunity to slide
it back many positions.
,
there is an opportunity to slide
it back many positions.
Note that we never move backwards through the text to compare a character
again - we slide the pattern forward accordingly.
The linearity of KMP follows from an amortized analysis.
Each time we move forward in the text we add 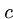 steps to our account,
while each mismatch costs us one step.
steps to our account,
while each mismatch costs us one step.
Provided the account never goes negative, we only did 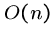 work total
since there were a total of
work total
since there were a total of 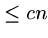 steps put in the account.
steps put in the account.
Thus if many consecutive mismatches requires the pattern to shift repeatedly,
it is only because we have enough previous forward moves to compensate.
There are ``improved'' failure functions which do even cleverer
preprocessing to reduce the number of pattern shifts.
However, such improvements have little effect in practice and are tricky
to program correctly.
The Boyer-Moore Algorithm
An alternate linear algorithm, Boyer-Moore, starts matching from
right side of the pattern instead of the left side:
pattern: ABCDABCD
text: ABCDABCE....
In this example, the last character in the window does not occur anywhere in the pattern.
Thus we can shift the pattern 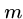 positions after one comparison.
positions after one comparison.
Thus the best case time for Boyer-Moore is sub-linear, i.e. 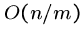 .
The worst-case is
.
The worst-case is 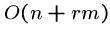 , where
, where 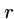 is the number of times the pattern
occurs in the text.
is the number of times the pattern
occurs in the text.
The algorithm precomputes a table of size 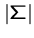 describing how far
to shift for a mismatch on each letter of the alphabet, i.e. depending
upon the position of the rightmost
occurrence of that letter in the pattern.
describing how far
to shift for a mismatch on each letter of the alphabet, i.e. depending
upon the position of the rightmost
occurrence of that letter in the pattern.
Further, since we know that the suffix of the pattern matched up to the
point of mismatch, we can precompute a table recording the next place
where the suffix occurs in the pattern.
We can use the bigger of the two shifts, since no intermediate
position can define a legal match.
Boyer-Moore may be the fastest algorithm for
alphanumeric string matching
in practice when implemented correctly.
Randomized String Matching
The Rabin-Karp algorithm computes an appropriate hash function on
all 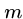 -length strings of the text, and does a brute force comparison
only if the hash value is the same for the text window and the pattern.
-length strings of the text, and does a brute force comparison
only if the hash value is the same for the text window and the pattern.
An appropriate hash function is
which treats each string as an 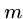 -digit base-
-digit base-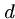 number, mod
number, mod 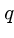 .
.
This hash function
can be computed incrementally in constant time
as we slide the window from left to right since
Further, if 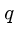 is a random prime the expected number of false positives
is small enough to yield a randomized linear algorithm.
is a random prime the expected number of false positives
is small enough to yield a randomized linear algorithm.
Multiple Exact Patterns
Many applications require searching a text for occurrences of any
one of many patterns, e.g. searching text for dirty words or
searching a genome for any one of a set of known motifs.
Pattern matching with wild card characters (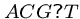 ) is an
important special case of multiple patterns.
) is an
important special case of multiple patterns.
Techniques from automata theory come into play, since any finite
set of patterns can be modeled by regular expressions, and
many interesting infinite sets (e.g. 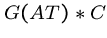 ) as well.
) as well.
The standard UNIX tool grep stands for ``general regular expression
pattern matcher''.
figure=figures/nano.eps,width=5.0in
The Aho-Corasick algorithm builds a DFA from the set of patterns and
then walks through the text in linear time, taking action when reaching
any accepting state.
Approximate String Comparison
An important generalization of exact string matching is measuring the
distance between two or more strings.
These problems arise naturally in biology because DNA / protein sequences
tend to be structurally conserved across species over the course of evolution,
so functionally similar genes in different organisms can be detected
via approximate string matching.
Computer science applications of approximate string matching included
spell checking and file difference testing.
A reasonable distance on strings measure minimizes the cost of the changes
which have to be made to convert one string to another.
There are three natural types of changes:
- Substitution
- Change a single character from pattern
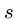 to a different character in text
to a different character in text 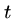 , e.g. `shot' to `spot'.
, e.g. `shot' to `spot'.
- Insertion
- Insert a single character into pattern
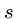 to help it match text
to help it match text 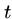 ,
e.g. `ago' to `agog'.
,
e.g. `ago' to `agog'.
- Deletion
- Delete a single character from pattern
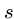 to help it match text
to help it match text 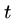 ,
e.g. `hour' to `our'.
,
e.g. `hour' to `our'.
Edit Distance and Similarity Scores
Computer scientists usually measure distance between strings 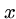 and
and 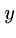 by the minimum number of insertions, deletions, and substitutions
to transform
by the minimum number of insertions, deletions, and substitutions
to transform 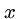 to
to 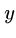 .
.
Certain mathematical properties are expected of any
distance measure, or metric:
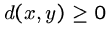 for all
for all 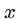 ,
, 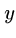 .
.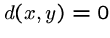 iff
iff 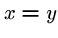 .
.-
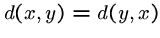 (symmetry)
(symmetry)
-
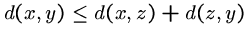 for all
for all 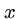 ,
, 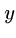 , and
, and 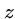 . (triangle inequality)
. (triangle inequality)
Biologists typically instead measure a sequence similarity score
which gets larger the more similar the sequences are.
Similar algorithms can be used to optimize both measures.
Pairwise String Alignment
An elegant algorithm for finding the minimum cost sequence of
changes to transform string 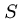 to string
to string 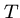 is based on the observation
that the correct action on the rightmost characters of
is based on the observation
that the correct action on the rightmost characters of 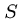 and
and 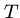 can
be computed knowing the costs of matching various prefixes:
can
be computed knowing the costs of matching various prefixes:
#define MATCH 0 /* symbol for match */
#define INSERT 1 /* symbol for insert */
#define DELETE 2 /* symbol for delete */
int string_compare(char *s, char *t, int i, int j)
{
int k; /* counter */
int opt[3]; /* cost of the three options */
int lowest_cost; /* lowest cost */
if (i == 0) return(j * indel(' '));
if (j == 0) return(i * indel(' '));
opt[MATCH] = string_compare(s,t,i-1,j-1) + match(s[i],t[j]);
opt[INSERT] = string_compare(s,t,i,j-1) + indel(t[j]);
opt[DELETE] = string_compare(s,t,i-1,j) + indel(s[i]);
lowest_cost = opt[MATCH];
for (k=INSERT; k<=DELETE; k++)
if (opt[k] < lowest_cost) lowest_cost = opt[k];
return( lowest_cost );
}
How much time does this program take?
Exponential in the length of the strings!
Dynamic Programming
Making this tractible requires realizing that we are repeatedly performing the
same computations on each pair of prefixes.
The entire state of the recursive call is governed by the index positions into
the strings.
Thus there are only
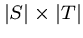 different calls.
different calls.
By storing the answers in a table and looking them up instead of recomputing,
the algorithm takes quadratic time.
Dynamic programming is the algorithmic technique of efficiently computing
recurrence relations by storing partial results.
It is very powerful on any ordered
structures, like character strings, permutations, and rooted trees.
The table data structure keeps track of the cost of reaching
this position plus the last move which took us to this cell.
typedef struct {
int cost; /* cost of reaching this cell */
int parent; /* parent cell */
} cell;
cell m[MAXLEN][MAXLEN]; /* dynamic programming table */
General Edit Distance via Dynamic Programming
Note how we use and update the table of partial results.
int string_compare(char *s, char *t)
{
int i,j,k; /* counters */
int opt[3]; /* cost of the three options */
for (i=0; i<MAXLEN; i++) {
row_init(i);
column_init(i);
}
for (i=1; i<strlen(s); i++)
for (j=1; j<strlen(t); j++) {
opt[MATCH] = m[i-1][j-1].cost + match(s[i],t[j]);
opt[INSERT] = m[i][j-1].cost + indel(t[j]);
opt[DELETE] = m[i-1][j].cost + indel(s[i]);
m[i][j].cost = opt[1];
m[i][j].parent = 1;
for (k=2; k<=3; k++)
if (opt[k] < m[i][j].cost) {
m[i][j].cost = opt[k];
m[i][j].parent = k;
}
}
goal_cell(s,t,&i,&j);
return( m[i][j].cost );
}
To determine the value of cell 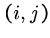 , we need the
the cells
, we need the
the cells 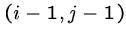 ,
, 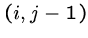 , and
, and 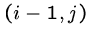 .
Any evaluation order with this property
will do, including the row-major order we used.
.
Any evaluation order with this property
will do, including the row-major order we used.
Standard String Edit Distance
The function string_compare is very general, and must be customized to a particular application.
It uses problem-specific subroutines match and indel to
return the costs of character pair transitions:
row_init(int i)
{
m[0][i].cost = i;
if (i>0)
m[0][i].parent=INSERT;
else
m[0][i].parent = -1;
}
|
column_init(int i)
{
m[i][0].cost = i;
if (i>0)
m[i][0].parent=DELETE;
else
m[0][i].parent = -1;
}
|
The functions row_init and column_init
to initialize the boundary conditions.
int match(char c, char d)
{
if (c == d) return(0);
else return(1);
}
|
int indel(char c)
{
return(1);
}
|
The function goal_cell returns the desired final
cell of interest in the matrix.
goal_cell(char *s, char *t, int *i, int *j)
{
*i = strlen(s) - 1;
*j = strlen(t) - 1;
}
Changing these functions lets us do substring matching, longest common
subsequence, and maximum monotone subsequence as special cases.
String Matching Example: Cost Matrix
The cost matrix in converting thou shalt not to you should not:
y o u - s h o u l d - n o t
: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
t: 1 1 2 3 4 5 6 7 8 9 10 11 12 13 13
h: 2 2 2 3 4 5 5 6 7 8 9 10 11 12 13
o: 3 3 2 3 4 5 6 5 6 7 8 9 10 11 12
u: 4 4 3 2 3 4 5 6 5 6 7 8 9 10 11
-: 5 5 4 3 2 3 4 5 6 6 7 7 8 9 10
s: 6 6 5 4 3 2 3 4 5 6 7 8 8 9 10
h: 7 7 6 5 4 3 2 3 4 5 6 7 8 9 10
a: 8 8 7 6 5 4 3 3 4 5 6 7 8 9 10
l: 9 9 8 7 6 5 4 4 4 4 5 6 7 8 9
t: 10 10 9 8 7 6 5 5 5 5 5 6 7 8 8
-: 11 11 10 9 8 7 6 6 6 6 6 5 6 7 8
n: 12 12 11 10 9 8 7 7 7 7 7 6 5 6 7
o: 13 13 12 11 10 9 8 7 8 8 8 7 6 5 6
t: 14 14 13 12 11 10 9 8 8 9 9 8 7 6 5
String Matching Example: Parent Matrix
y o u - s h o u l d - n o t
: -1 2 2 2 2 2 2 2 2 2 2 2 2 2 2
t: 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1
h: 3 1 1 1 1 1 1 2 2 2 2 2 2 2 2
o: 3 1 1 1 1 1 1 1 2 2 2 2 2 1 2
u: 3 1 3 1 2 2 2 2 1 2 2 2 2 2 2
-: 3 1 3 3 1 2 2 2 2 1 1 1 2 2 2
s: 3 1 3 3 3 1 2 2 2 2 1 1 1 1 1
h: 3 1 3 3 3 3 1 2 2 2 2 2 2 1 1
a: 3 1 3 3 3 3 3 1 1 1 1 1 1 1 1
l: 3 1 3 3 3 3 3 1 1 1 2 2 2 2 2
t: 3 1 3 3 3 3 3 1 1 1 1 1 1 1 1
-: 3 1 3 3 1 3 3 1 1 1 1 1 2 2 2
n: 3 1 3 3 3 3 3 1 1 1 1 3 1 2 2
o: 3 1 1 3 3 3 3 1 1 1 1 3 3 1 2
t: 3 1 3 3 3 3 3 3 1 1 1 3 3 3 1
Reconstructing the Alignment
Once we have the dynamic programming matrix, we have to walk backwards
through it to reconstruct the alignment.
Either explicit back pointers can be kept, or we can remake decisions of
how we got to the critical cells starting from the back.
reconstruct_path(char *s, char *t, int i, int j)
{
if (m[i][j].parent == -1) return;
if (m[i][j].parent == MATCH) {
reconstruct_path(s,t,i-1,j-1);
match_out(s, t, i, j);
return;
}
if (m[i][j].parent == INSERT) {
reconstruct_path(s,t,i,j-1);
insert_out(t,j);
return;
}
if (m[i][j].parent == DELETE) {
reconstruct_path(s,t,i-1,j);
delete_out(s,i);
return;
}
}
The actions we take on traceback are governed by
match_out, insert_out, and delete_out:
insert_out(char *t, int j)
{
printf("I");
}
delete_out(char *s, int i)
{
printf("D");
}
|
match_out(char *s,char *t,int i,int j)
{
if (s[i] == t[j]) printf("M");
else printf("S");
}
|
The edit sequence from ``thou-shalt-not'' to ``you-should-not''
is DSMMMMMISMSMMMM - meaning delete the first `t', replace the `h' with `y',
match the next five characters before inserting an `o', replace `a' with 'u',
replace the `t' with a `d'.
Other Applications: Longest Common Subsequence
By changing the relative costs for matching and substitution we can
get different alignments.
If we make the cost of substitution so high as to be greater than the cost
of inserting and deleting characters, the returned alignment will seek
only to match the largest number of possible characters, returning the
longest common subsequence.
int match(char c, char d)
{
if (c == d) return(0);
else return(MAXLEN);
}
This shows us that the exact replacement costs can have a big impact on
the optimal alignment.
By changing our traceback functions we get different behavior:
insert_out(char *t,int j)
{
}
delete_out(char *s,int i)
{
}
|
match_out(char *s,char *t,
int i,int j)
{
if (s[i]==t[j])
printf("%c",s[i]);
}
|
abracadabra
abbababa
length of longest common subsequence = 6
abaaba
Substring Matching
Suppose we want to search for a short pattern (say `Skiena' allowing mispellings)
in a long text.
Using the approximate string matching function will achieve little sensitivity,
since most of the edit cost will be deleting the body of the full text.
We can use the same basic edit distance function for this task, but must adjust
the initialization so that the substring matches in the middle of the text are
not discouraged:
row_init(int i) /* what is m[0][i]? */
{
m[0][i].cost = 0; /* NOTE CHANGE */
m[0][i].parent = -1; /* NOTE CHANGE */
}
Now the goal cell is the cheapest cell matching the entire pattern:
goal_cell(char *s, char *t, int *i, int *j)
{
int k; /* counter */
*i = strlen(s) - 1;
*j = 0;
for (k=1; k<strlen(t); k++)
if (m[*i][k].cost < m[*i][*j].cost) *j = k;
}
Biological Sequence Comparison
Constructing a meaningful alignment of two sequences requires using
a appropriate function to measure the cost of changing between
each possible pair symbols.
In correcting text entered by a fast typist, we might penalize pairs of
symbols near each other on the keyboard less than those on different sides,
for example.
For genomic sequences, the weights/scores governing the cost of changing
between bases are given by PAM matrices for ``point accepted mutations''
DNA PAM matrices include Blast similarity
and transition / transversion matrices.
A T C G A T C G
A 5 -4 -4 -4 A 0 5 5 1
T -4 5 -4 -4 T 5 0 1 5
C -4 -4 5 -4 C 5 1 0 5
G -4 -4 -4 5 G 1 5 5 0
The four nucleotide bases are classified as either
purines (Adenine and Guanine) or pyrimidines (Cytosine and Thymine).
Transitions are mutations which stay within the class (e.g. A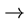 G or C
G or C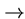 T),
while transversions cross classes (e.g. A
T),
while transversions cross classes (e.g. A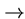 C, A
C, A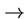 T etc.).
T etc.).
Transitions are more common than transversions.
Genetic Code Matrix
The following genetic code matrix calculates the minimum number
of DNA base changes to go from a codon for 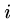 to a codon for
to a codon for 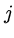 .
.
Met Tyr requires all 3 positions to change.
Tyr requires all 3 positions to change.
A S G L K V T P E D N I Q R F Y C H M W Z B X
A 0 1 1 2 2 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2
S 1 0 1 1 2 2 1 1 2 2 1 1 2 1 1 1 1 2 2 1 2 2 2
G 1 1 0 2 2 1 2 2 1 1 2 2 2 1 2 2 1 2 2 1 2 2 2
L 2 1 2 0 2 1 2 1 2 2 2 1 1 1 1 2 2 1 1 1 2 2 2
K 2 2 2 2 0 2 1 2 1 2 1 1 1 1 2 2 2 2 1 2 1 2 2
V 1 2 1 1 2 0 2 2 1 1 2 1 2 2 1 2 2 2 1 2 2 2 2
T 1 1 2 2 1 2 0 1 2 2 1 1 2 1 2 2 2 2 1 2 2 2 2
P 1 1 2 1 2 2 1 0 2 2 2 2 1 1 2 2 2 1 2 2 2 2 2
E 1 2 1 2 1 1 2 2 0 1 2 2 1 2 2 2 2 2 2 2 1 2 2
D 1 2 1 2 2 1 2 2 1 0 1 2 2 2 2 1 2 1 2 2 2 1 2
N 2 1 2 2 1 2 1 2 2 1 0 1 2 2 2 1 2 1 2 2 2 1 2
I 2 1 2 1 1 1 1 2 2 2 1 0 2 1 1 2 2 2 1 2 2 2 2
Q 2 2 2 1 1 2 2 1 1 2 2 2 0 1 2 2 2 1 2 2 1 2 2
R 2 1 1 1 1 2 1 1 2 2 2 1 1 0 2 2 1 1 1 1 2 2 2
F 2 1 2 1 2 1 2 2 2 2 2 1 2 2 0 1 1 2 2 2 2 2 2
Y 2 1 2 2 2 2 2 2 2 1 1 2 2 2 1 0 1 1 3 2 2 1 2
C 2 1 1 2 2 2 2 2 2 2 2 2 2 1 1 1 0 2 2 1 2 2 2
H 2 2 2 1 2 2 2 1 2 1 1 2 1 1 2 1 2 0 2 2 2 1 2
M 2 2 2 1 1 1 1 2 2 2 2 1 2 1 2 3 2 2 0 2 2 2 2
W 2 1 1 1 2 2 2 2 2 2 2 2 2 1 2 2 1 2 2 0 2 2 2
Z 2 2 2 2 1 2 2 2 1 2 2 2 1 2 2 2 2 2 2 2 1 2 2
B 2 2 2 2 2 2 2 2 2 1 1 2 2 2 2 1 2 1 2 2 2 1 2
X 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
Hydrophobicity Matrix
Amino acids differ to the extent that they like ( hydrophilic)
or don't like ( hydrophobic) water.
Hydrophobic residues do not want to be on the surface of a protein.
R K D E B Z S N Q G X T H A C M P V L I Y F W
R 10 10 9 9 8 8 6 6 6 5 5 5 5 5 4 3 3 3 3 3 2 1 0
K 10 10 9 9 8 8 6 6 6 5 5 5 5 5 4 3 3 3 3 3 2 1 0
D 9 9 10 10 8 8 7 6 6 6 5 5 5 5 5 4 4 4 3 3 3 2 1
E 9 9 10 10 8 8 7 6 6 6 5 5 5 5 5 4 4 4 3 3 3 2 1
B 8 8 8 8 10 10 8 8 8 8 7 7 7 7 6 6 6 5 5 5 4 4 3
Z 8 8 8 8 10 10 8 8 8 8 7 7 7 7 6 6 6 5 5 5 4 4 3
S 6 6 7 7 8 8 10 10 10 10 9 9 9 9 8 8 7 7 7 7 6 6 4
N 6 6 6 6 8 8 10 10 10 10 9 9 9 9 8 8 8 7 7 7 6 6 4
Q 6 6 6 6 8 8 10 10 10 10 9 9 9 9 8 8 8 7 7 7 6 6 4
G 5 5 6 6 8 8 10 10 10 10 9 9 9 9 8 8 8 8 7 7 6 6 5
X 5 5 5 5 7 7 9 9 9 9 10 10 10 10 9 9 8 8 8 8 7 7 5
T 5 5 5 5 7 7 9 9 9 9 10 10 10 10 9 9 8 8 8 8 7 7 5
H 5 5 5 5 7 7 9 9 9 9 10 10 10 10 9 9 9 8 8 8 7 7 5
A 5 5 5 5 7 7 9 9 9 9 10 10 10 10 9 9 9 8 8 8 7 7 5
C 4 4 5 5 6 6 8 8 8 8 9 9 9 9 10 10 9 9 9 9 8 8 5
M 3 3 4 4 6 6 8 8 8 8 9 9 9 9 10 10 10 10 9 9 8 8 7
P 3 3 4 4 6 6 7 8 8 8 8 8 9 9 9 10 10 10 9 9 9 8 7
V 3 3 4 4 5 5 7 7 7 8 8 8 8 8 9 10 10 10 10 10 9 8 7
L 3 3 3 3 5 5 7 7 7 7 8 8 8 8 9 9 9 10 10 10 9 9 8
I 3 3 3 3 5 5 7 7 7 7 8 8 8 8 9 9 9 10 10 10 9 9 8
Y 2 2 3 3 4 4 6 6 6 6 7 7 7 7 8 8 9 9 9 9 10 10 8
F 1 1 2 2 4 4 6 6 6 6 7 7 7 7 8 8 8 8 9 9 10 10 9
W 0 0 1 1 3 3 4 4 4 5 5 5 5 5 6 7 7 7 8 8 8 9 10
PAM Matrices
This variety of possible matrix criteria make judging the significance
of an alignment tricky.
Most widely used are PAM matrices, for ``point accepted mutations''.
These were constructed by aligning very similar proteins, and tabulating
how often each substitution occurred.
The PAM1 matrix scores the transitions when the proteins differ in 1%
of the residues.
Raising this to higher powers gives us PAM matrices suited for comparing
more distantly related proteins.
figure=figures/pam50.eps,width=3.5in
figure=figures/pam250.eps,width=3.5in
Note the main diagonal on these plots of the PAM50 and PAM250 matrices.
More modern than the PAM matrices are the Blosum matrices,
reflecting additional sequence alignment data.
Local Alignment
The critical problem of biological interest is in comparing two long sequences and finding
local areas of similarity.
Typical applications include (1) what regions have been conserved between mouse and human,
and (2) recognizing coding regions in `split genes'.
Here using similarity scores is more meaningful than edit distance.
We want 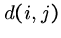 to be the highest-scoring local alignment ending at
to be the highest-scoring local alignment ending at ![$S[i]$](img68.gif) and
and ![$T[j]$](img69.gif) .
.
This way to compute this is typically called the Smith-Waterman algorithm.
It is the same basic algorithm as for edit distance, except:
- We maximize instead of minimize.
- We have the option of starting our local alignment fresh at each cell in the matrix, i.e.
0 is always an allowable cost.
- We scan all
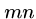 cells at the end to see which gives us the best score, not just those
along the last row or column.
cells at the end to see which gives us the best score, not just those
along the last row or column.
Smith-Waterman Program
int smith_waterman(char *s, char *t)
{
int i,j,k; /* counters */
int opt[3]; /* cost of the three options */
int match(); int indel();
for (i=0; i<=strlen(s); i++)
for (j=0; j<=strlen(t); j++)
cell_init(i,j);
for (i=1; i<strlen(s); i++)
for (j=1; j<strlen(t); j++) {
opt[MATCH] = m[i-1][j-1].cost + match(s[i],t[j]);
opt[INSERT] = m[i][j-1].cost + indel(t[j]);
opt[DELETE] = m[i-1][j].cost + indel(s[i]);
m[i][j].cost = 0;
m[i][j].parent = -1;
for (k=MATCH; k<=DELETE; k++)
if (opt[k] > m[i][j].cost) {
m[i][j].cost = opt[k];
m[i][j].parent = k;
}
}
goal_cell(s,t,&i,&j);
return( m[i][j].cost );
}
Supporting Routines
goal_cell(char *s, char *t, int *x, int *y)
{
int i,j; /* counters */
*x = *y = 0;
for (i=0; i<strlen(s); i++)
for (j=0; j<strlen(t); j++)
if (m[i][j].cost > m[*x][*y].cost) {
*x = i;
*y = j;
}
}
int match(char c, char d)
{
if (c == d) return(+5);
else return(-4);
}
int indel(char c)
{
return(-4);
}
cell_init(int i, int j)
{
m[i][j].cost = 0;
m[i][j].parent = -1;
}
Smith-Waterman Example
Note how the maximum score (31) is not achieved with the
exact match public but includes the preceeding blank.
This is because we score a match more than we penalize a mismatch/indel.
b e a t _ r e p u b l i c a n s
: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
f: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
o: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
r: 0 0 0 0 0 0 5 1 0 0 0 0 0 0 0 0 0
_: 0 0 0 0 0 5 1 1 0 0 0 0 0 0 0 0 0
t: 0 0 0 0 5 1 1 0 0 0 0 0 0 0 0 0 0
h: 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0
e: 0 0 5 1 0 0 0 5 1 0 0 0 0 0 0 0 0
_: 0 0 1 1 0 5 1 1 1 0 0 0 0 0 0 0 0
p: 0 0 0 0 0 1 1 0 6 2 0 0 0 0 0 0 0
u: 0 0 0 0 0 0 0 0 2 11 7 3 0 0 0 0 0
b: 0 5 1 0 0 0 0 0 0 7 16 12 8 4 0 0 0
l: 0 1 1 0 0 0 0 0 0 3 12 21 17 13 9 5 1
i: 0 0 0 0 0 0 0 0 0 0 8 17 26 22 18 14 10
c: 0 0 0 0 0 0 0 0 0 0 4 13 22 31 27 23 19
_: 0 0 0 0 0 5 1 0 0 0 0 9 18 27 27 23 19
g: 0 0 0 0 0 1 1 0 0 0 0 5 14 23 23 23 19
o: 0 0 0 0 0 0 0 0 0 0 0 1 10 19 19 19 19
o: 0 0 0 0 0 0 0 0 0 0 0 0 6 15 15 15 15
d: 0 0 0 0 0 0 0 0 0 0 0 0 2 11 11 11 11
Gap Penalties
Gaps in sequence alignments occur for several reasons, including
(1) the deletion of introns from split genes, (2) the insertion of
mobile sequence elements such as transposons, (3) because conserved
parts of a protein may include several relatively small docking sites.
Gap in alignments can be modeled as repeated base deletions,
where the penalty for a gap is just a linear function of its length.
However, in many applications (e.g. exons/introns, extracting good quotes for
the back of a book jacket) the length of the gap
is relatively unimportant.
Thus a more meaningful model charges a fixed penalty for the existence
of each gap, plus another penalty depending upon the length of the
gap.
Affine gap penalties are 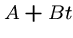 for gaps of length
for gaps of length 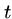 ,
while logarithmic gap penalties of the form
,
while logarithmic gap penalties of the form 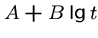 are
suggested by empirical data.
are
suggested by empirical data.
Arbitrary Gap Weights
Suppose the gap cost is a completely general function of length for which
we cannot assume monotonicity or any other property.
Then we must explicitly try every possible length deletion/insertion at
every possible position, i.e. 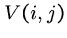 takes the best of the following options:
takes the best of the following options:
Because we are doing a linear amount of work for each cell, the
time complexity goes to
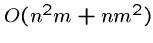 or
or 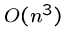 if
if 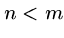 .
.
This algorithm is often called Needleman-Wunsch.
Affine Gap Weights
By being clever we can avoid the extra linear cost of
looking for the start of the gap for affine gap penalties,
i.e. penalties of the form 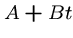 for gaps of length
for gaps of length 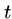
We will use the insertion and deletion recurrences 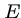 and
and 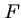 to
encode the cost of being in gap mode, meaning we have already paid the
cost of initiating the gap.
to
encode the cost of being in gap mode, meaning we have already paid the
cost of initiating the gap.
With constant amount of work per cell, this algorithm takes 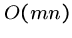 time,
same as without gap costs.
time,
same as without gap costs.
The default in FASTA sets 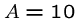 and
and 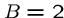 , so starting a gap costs
the equivalent of five deletions.
, so starting a gap costs
the equivalent of five deletions.
The special case of convex penalty functions (including logarithmic
costs) can be solved in
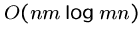 time with a more complicated
algorithm.
time with a more complicated
algorithm.
Space Efficient Dynamic Programming
Quadratic space will kill you faster than quadratic time.
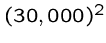 bytes equals one gigabyte, while
bytes equals one gigabyte, while 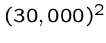 operations
takes 1000 seconds on a machine doing 1 million steps per second.
operations
takes 1000 seconds on a machine doing 1 million steps per second.
The dynamic programming algorithms we have seen only look
at neighboring rows/columns to make their decision.
Computing the highest cell score in the matrix does
not require keeping more than then last column and the best value
to date, for a total of 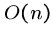 space, where
space, where 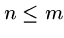 .
.
Note that reconstructing
the optimal alignment does seem to require keeping the entire matrix,
however.
But Hirshberg found a clever way to reconstruct the alignment in 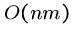 time using only
time using only 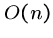 space, by recomputing the appropriate portions
of the matrix.
space, by recomputing the appropriate portions
of the matrix.
For each cell, we drag along the row number where the optimal path
to in crossed the middle (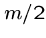 nd) column.
nd) column.
This requires only 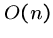 extra memory, one cell per row.
extra memory, one cell per row.
This works because the crossing point 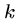 of the
of the 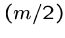 nd column
means that the optimal alignment lies in the sub matrices
nd column
means that the optimal alignment lies in the sub matrices 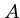 from (1,1) to
from (1,1) to
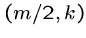 , and
, and 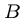 from
from 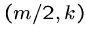 to
to 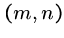 .
.
Note that the number of cells in 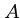 and
and 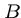 totals only half of the the
original
totals only half of the the
original 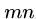 cells.
cells.
Further, these dynamic programming algorithms are linear in the number
of cells they compute.
Thus the total amount of recomputation done is
so the total work remains 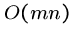
Heuristic String Comparison
Dynamic programming methods for sequence alignment give the highest
quality results.
However, quadratic 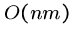 algorithms are only feasible for comparing
two modest sized sequences.
algorithms are only feasible for comparing
two modest sized sequences.
Comparing the human genome against mouse with a quadratic algorithm
(
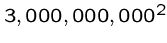 operations)
at a billion operations per second equals 285 years!
operations)
at a billion operations per second equals 285 years!
Comparing your target sequence against the entire database is hopeless,
even with special purpose hardware.
Instead, heuristic algorithms such as BLAST and FASTA are used
to make an initial scan of the database to find a small number
of hits.
Smith-Waterman can then be used to find the optimal alignment to display.
FASTA
FASTA is a heuristic string alignment program which is based upon
finding short exact matches (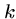 -mers) between the query sequence
and the database.
-mers) between the query sequence
and the database.
The trick is to choose 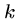 large enough that there are relatively
few hits, but small enough that we are likely to have an exact
large enough that there are relatively
few hits, but small enough that we are likely to have an exact
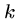 -mer match between related sequences.
-mer match between related sequences.
Recommended values of 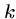 are 2 for protein sequences and 6 for
DNA sequences.
are 2 for protein sequences and 6 for
DNA sequences.
Note that there are at most 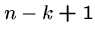 distinct
distinct 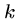 -mers in a sequence of
length
-mers in a sequence of
length 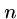 .
.
A hash table of all 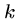 -mers in the database can be built once
and used repeatedly for efficiently looking up the
-mers in the database can be built once
and used repeatedly for efficiently looking up the 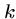 -mers
in query strings.
-mers
in query strings.
A dynamic programming-like algorithm is used to align the 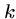 -mer
hits between query and database, but the problem is much smaller
since there are far fewer hits than bases.
-mer
hits between query and database, but the problem is much smaller
since there are far fewer hits than bases.
BLAST
BLAST stands for ``Basic Local Alignment Search Tool''.
It also seeks to exploit the speed of exact pattern matching
while factoring in the impact of the scoring matrix.
BLAST also breaks the query into 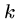 -mers in order to search
a hash table, but for input
-mers in order to search
a hash table, but for input 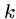 -mer
-mer 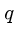 constructs all other
constructs all other
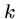 -mers which lie within a distance
-mers which lie within a distance 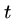 of
of 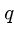 .
.
By processing all these patterns into an automata, BLAST can
then make one linear-time pass through the database
to find all exact matches and group them in an alignment.
The window size 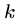 is typically 3-5 for protein sequences and 12 for DNA
sequences.
is typically 3-5 for protein sequences and 12 for DNA
sequences.
Conventional wisdom has BLAST as faster than FASTA, but perhaps
a little less accurate.
Using Blast
Several variants of the Basic Local Alignment Search Tool are available at www.ncbi.nlm.nih.gov/BLAST/
- blastp
- amino acid query sequence to protein sequence database
- blastn
- nucleotide query sequence to nucleotide sequence database
- blastx
- nucleotide query sequence translated in all reading frames against a
protein sequence database
- tblastn
- protein query sequence against nucleotide sequence database translated
in all reading frames
- tblastx
- most intensive computationally;
compares 6 frame translations of nucleotides query sequence against 6
frame translation of nucleotide sequence database
You can download your own local copy of the code and databases, or use web resources.
Databases
Database choices include:
- nr
- all non-redundant sequences (from particular databases)
- est
- expressed-sequence tags (RNA from expressed genes) in human, mouse, etc.
- month
- new releases from the past 30 days
- genomes
- from Drosophila, yeast, E.coli, human, etc.
Your query sequence can be (1) an amino acid or nucleotide sequence you type or paste in, or (2) the
accession or GI number of Genbank entry.
There are a wide range of output formats.
Advanced Search Parameters
You can select the organism you are interested in to limit your search.
You can change the expect value 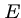 , the threshold for reporting matches against a database sequence.
The default threshold of 10 means that 10 matches are expected to be found merely by chance (Karlin and Altschul).
Lower expect thresholds are more stringent, leading to fewer chance matches being reported.
, the threshold for reporting matches against a database sequence.
The default threshold of 10 means that 10 matches are expected to be found merely by chance (Karlin and Altschul).
Lower expect thresholds are more stringent, leading to fewer chance matches being reported.
The expect value decreases exponentially with the alignment score 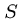 .
.
You can use filter to masks sequences of low compositional complexity, i.e. eliminate statistically
significant but biologically uninteresting reports.
You can select the cost comparison matrix.
The default is BLOSUM62, but with this matrix fairly long alignments are requires to rise above background.
PAM matrices are recommends if search for short alignments.
Significance Scores
To assess whether a given alignment constitutes evidence for homology, it
helps to know how strong an alignment can be expected from chance alone.
A model for expected number of high-scoring segment pairs (HSPs) with score at least 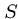 is
is
where 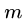 and
and 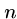 are the sequence lengths and
are the sequence lengths and 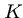 and
and  are scaling parameters.
are scaling parameters.
Doubling length of either sequence doubles 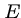 , as it should.
, as it should.
Doubling the score for an HSP to 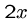 requires it to attain the score x twice in a row,
so
requires it to attain the score x twice in a row,
so 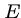 should decrease exponentially with score.
should decrease exponentially with score.
The number of random HSPs with score 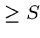 is described by a Poisson
distribution, so the probability of finding exactly
is described by a Poisson
distribution, so the probability of finding exactly 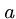 HSPs with
score
HSPs with
score 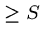 is given by
is given by
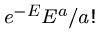 .
.
Hence the probability of finding 0 HSPs is 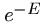 , and the probability of
finding at least one is
, and the probability of
finding at least one is 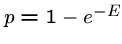 .
This is the p-value of the score.
.
This is the p-value of the score.
A statistical method to measure significance is to generate many
random sequence pairs of the appropriate length and composition, and calculate
the optimal alignment score for each.


Next: About this document ...
Up: My Home Page
Steve Skiena
2002-10-08