1.4.10 Drawing Graphs Nicely
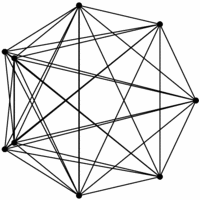
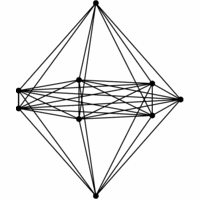
INPUT OUTPUT
Input Description:
A graph G.
Problem:
Give a drawing of graph G which accurately reflects its structure.
Excerpt from
The Algorithm Design Manual:
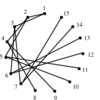
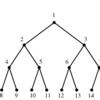
Drawing graphs nicely is a problem that constantly arises in applications, such as displaying file directory trees or
circuit schematic diagrams.Yet it is inherently ill-defined.
What exactly does nicely mean? We seek an algorithm that shows off the structure of
the graph so the viewer can best understand it. We also seek a drawing that looks aesthetically pleasing.
Unfortunately, these are ``soft'' criteria for which it is impossible to design an optimization algorithm.
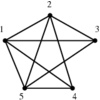
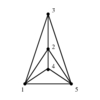
Indeed, it is possible to come up with two or more radically different drawings of certain graphs
and have each be most appropriate in certain contexts.
Several ``hard'' criteria can partially measure the quality of a drawing:
- Crossings -- We seek a drawing with as few pairs of crossing edges as possible,
since they are distracting.
- Area -- We seek a drawing that uses as little paper as possible,
while ensuring that no pair of vertices are placed too close to each other.
- Edge Length -- We seek a drawing that avoids long edges, since they tend to obscure
other features of the drawing.
- Aspect Ratio -- We seek a drawing whose aspect ratio (width/height) reflects
that of the desired output medium (typically a computer screen at 4/3) as close
as possible.
Unfortunately, these goals are mutually contradictory, and
the problem of finding the best drawing under
any nonempty subset of them will likely be NP-complete.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com




 Handbook of Graph Drawing and Visualization
Handbook of Graph Drawing and Visualization Exploratory Social Network Analysis with Pajek
Exploratory Social Network Analysis with Pajek Drawing Graphs: Methods and Models
Drawing Graphs: Methods and Models Graph Drawing: Algorithms for the Visualization of Graphs
Graph Drawing: Algorithms for the Visualization of Graphs Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica