1.1.5 Set Data Structures
INPUT OUTPUT
Input Description:
A universe of objects U = \{ u_1,...,u_n\},
and a collection of subsets S_1,...,S_m, S_i \subset U.
Problem:
Represent each subset so as to efficiently (1) test whether u_i \in S_j,
(2) find the union or intersection of S_i and S_j, (3) insert or delete
members of S_i.
Excerpt from
The Algorithm Design Manual:
We distinguish sets from two other kinds of objects: strings and dictionaries.
If there is no fixed-size universal set, a collection of objects is best
thought of as a dictionary. If the order does matter in a subset, i.e. if {A,B,C} is not the same
as {B,C,A}, then your structure is more profitably thought of as a string.
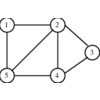
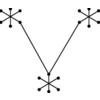
When each subset has cardinality exactly two, they form edges in a graph whose vertices are the universal set.
A system of subsets with no restrictions on the cardinality of its members is called a hypergraph. It
often can be profitable to consider whether your problem has a graph-theoretical analogy, like connected
components or shortest path in a hypergraph.
Your primary alternatives for representing arbitrary systems of subsets are:
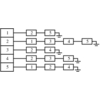
- Bit Vectors If your universal set U contains n items, an n-bit vector or array
can represent any subset S subset of U. Bit i will be 1 if i is contained in S, otherwise bit i is 0.
Since only one bit is used per element, bit vectors can be very space efficient for surprisingly large values of
|U|. Element insertion and deletion simply flips the appropriate bit. Intersection and union are done by
``and-ing'' or ``or-ing'' the bits together. The only real drawback of a bit vector is that for sparse subsets,
it takes O(n) time to explicitly identify all members of S.
- Containers or dictionaries A subset can also be represented using a linked list, array, binary
tree, or dictionary containing exactly the elements in the subset. No notion of a fixed universal set is needed
for such a data structure. For sparse subsets, dictionaries can be more space and time efficient than bit vectors
and easier to work with and program. For efficient union and intersection operations, it pays to keep the elements
in each subset sorted, so a linear-time traversal through both subsets identifies all duplicates.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com


 Data Structures and Algorithm Analysis in C++ (3rd Edition)
Data Structures and Algorithm Analysis in C++ (3rd Edition) Algorithms in C++: Fundamentals, Data Structures, Sorting, Searching
Algorithms in C++: Fundamentals, Data Structures, Sorting, Searching The Art of Computer Programming: Fundamental Algorithms
The Art of Computer Programming: Fundamental Algorithms Davenport-Schinzel sequences and their geometric applications
Davenport-Schinzel sequences and their geometric applications Data Structures and Network Algorithms
Data Structures and Network Algorithms