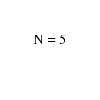1.3.5 Generating Subsets
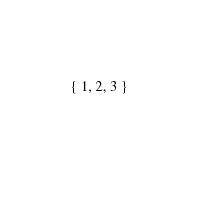
INPUT OUTPUT
Input Description:
An integer n.
Problem:
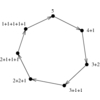
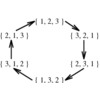
Generate (1) all, or (2) a random, or (3) the next subset
of the integers 1 to n.
Excerpt from
The Algorithm Design Manual:
A subset describes a selection of objects, where the order among them does not matter. Many of the algorithmic
problems in this catalog seek the best subset of a group of things: vertex cover seeks the smallest subset of
vertices to touch each edge in a graph; knapsack seeks the most profitable subset of items of bounded total
size; and set packing seeks the smallest subset of subsets that together cover each item exactly once.
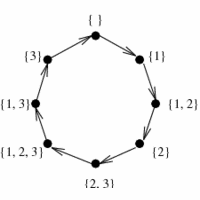
There are 2n distinct subsets of an $n$-element set, including the empty set as well as the
set itself. This grows exponentially, but at a considerably smaller rate than the $n!$ permutations of
n items. Indeed, since 220 = 1,048,576, a brute-force search through all subsets of
20 elements is easily manageable, although by n=30, 230 = 1,073,741,824, so you will
certainly be pushing things.
Recommended Books
Related Links
The fxt demos: combinatorics demos
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com


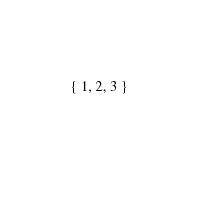

 The Art of Computer Programming, Volume 4 Fascicle 3: Generating All Combinations and Partitions
The Art of Computer Programming, Volume 4 Fascicle 3: Generating All Combinations and Partitions Combinatorial Algorithms : Generation, Enumeration, and Search
Combinatorial Algorithms : Generation, Enumeration, and Search Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica Combinatorial Algorithms: an update
Combinatorial Algorithms: an update Combinatorial Algorithms for Computers and Calculators
Combinatorial Algorithms for Computers and Calculators